Instructions to do the cross result of two vectors
We will likewise clarify what this condition means and how to utilize it in a basic yet precise manner. Before we present the recipe for the vector item, we need two vectors that we will call an and b. These two vectors ought not be collinear (a.k.a. ought not be equal) for reasons that we will clarify subsequently. In this way, right away, how about we see the cross product calculator
c = a × b = |a| * |b| * sinθ *
The factor of oppositeness along with the sinus work present in the recipe are acceptable markers of the mathematical understandings of the vector cross item. We will speak more about these in the following areas. You can likewise observe why it is urgent that the two vectors an and b are not equal. On the off chance that they were equal, it would prompt a zero point between them (θ = 0). Henceforth, both sin θ and c would be equivalent to zero, which is an extremely tiresome outcome. Likewise fascinating to note is the way that a basic stage of an and b would alter just the course of c since - sin(θ) = sin(-
We have seen the numerical recipe for the vector cross item, yet you may even now be thinking "This is just fine yet how would I really ascertain the new vector?" And that is an amazing inquiry! The quickest and most effortless arrangement is to utilize our vector cross item mini-computer, in any case, in the event that you have perused this far, you are likely looking for results as well as for information. We can separate the cycle into 3 unique advances: ascertaining the modulus of a vector, computing the point between two vectors, and figuring the opposite unitary vector. Putting all these three mediator results together by methods for a straightforward augmentation will yield the ideal vector. Figuring points between vectors may get excessively convoluted in 3-D space; and, if all we need to do is to realize how to ascertain the cross item between two vectors, it probably won't merit the problem.
All things considered, how about we investigate a more direct and commonsense method of ascertaining the vector cross item by methods for an alternate cross item equation. This new recipe utilizes the decay of a 3D vector into its 3 parts. This is an extremely basic approach to portray and work with vectors in which every segment speaks to a course in space and the number going with it speaks to the length of the vector the particular way. Standardly, the three components of the 3-D space we're working with are named x, y and z and are spoken to by the unitary vectors I, j and k separately. Following this terminology, every vector can be spoken to by an amount of these three unitary vectors. The vectors are commonly discarded for brevities purpose however are as yet suggested and have a major bearing on the consequence of the cross item.
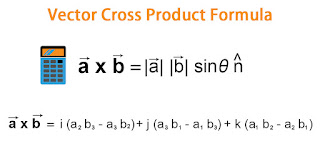
Comments
Post a Comment